
 Четырёхугольник ABCD со сторонами AB=19 и CD=28 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠
AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Четырёхугольник ABCD со сторонами AB=19 и CD=28 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠
AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Вариант №1 (предложил пользователь Всеволод).
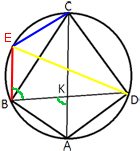 Проведем BE||AC
Проведем BE||AC
ABCE - трапеция по
определению.
Так как эта
трапеция вписана в окружность, то данная
трапеция равнобедренная (по
свойству описанной окружности).
Следовательно EC=AB=19.
∠AKB=∠KBE=60°, т.к. это
накрест лежащие углы при параллельных прямых BE и AC.
BECD - четырехугольник, вписанный в окружность, следовательно:
∠ECD+∠KBE=180° (по
свойству).
∠ECD=180°-∠KBE=180°-60°=120°
Применим
теорему косинусов для треугольника CDE:
ED2=EC2+CD2-2*EC*CD*cos∠ECD
ED2=192+282-2*19*28*cos120°
ED2=361+784-2*19*28*(-1/2)
ED2=1145+532=1677
ED=√
А теперь применим
теорему синусов для треугольника CDE:
ED/sin∠ECD=2R
R=√
Ответ: R=√
 Пусть R - радиус окружности.
Пусть R - радиус окружности.Поделитесь решением
Присоединяйтесь к нам...
 Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды
CD, если AB=12, CD=16, а расстояние от центра окружности до хорды AB равно 8.
Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды
CD, если AB=12, CD=16, а расстояние от центра окружности до хорды AB равно 8.
 Периметр квадрата равен 184. Найдите площадь квадрата.
Периметр квадрата равен 184. Найдите площадь квадрата.
 В треугольнике ABC DE – средняя линия. Площадь треугольника CDE равна 35. Найдите площадь треугольника ABC.
В треугольнике ABC DE – средняя линия. Площадь треугольника CDE равна 35. Найдите площадь треугольника ABC.
Какие из данных утверждений верны? Запишите их номера.
1) Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники подобны.
2) В любой четырёхугольник можно вписать окружность.
3) Центром описанной окружности треугольника является точка пересечения серединных перпендикуляров к его сторонам.
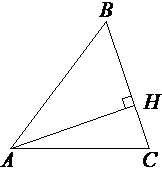 В остроугольном треугольнике ABC высота AH равна 20√
В остроугольном треугольнике ABC высота AH равна 20√
Комментарии: