
 В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 208. Найдите стороны треугольника ABC.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 208. Найдите стороны треугольника ABC.
Вариант №1
Рассмотрим треугольник ABD.
BO перпендикулярен AD (по условию задачи), т.е. ∠BOD=∠BOA=90°.
∠ABO=∠DBO (т.к. BE -
биссектриса).
Получается, что треугольники ABO и DBO равны (по
второму признаку равенства треугольников).
Следовательно, AB=BD.
Т.е. треугольник ABD -
равнобедренный.
BO -
биссектриса этого треугольника, следовательно и
медиана, и
высота (по третьему
свойству равнобедренного треугольника).
Следовательно, AO=OD=AD/2=208/2=104.
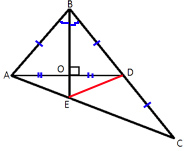 Проведем отрезок ED и рассмотрим треугольник BEC.
Проведем отрезок ED и рассмотрим треугольник BEC.
ED -
медиана этого треугольника, так как делит сторону BC пополам.
Площади треугольников EDC и EDB равны (по второму
свойству медианы). SEDC=SEDB=(BE*OD)/2=(208*104)/2=104*104=10816
SABE=(BE*AO)/2=(208*104)/2=10816
Т.е. SABE=SEDC=SEDB=10816
Тогда, SABС=3*10816=32448
AD -
медиана треугольника ABC (по условию), следовательно делит треугольник на два равных по площади треугольника ABD и ACD (по
второму свойству медианы).
SABD=(AD*BO)/2=SABC/2
(208*BO)/2=32448/2
BO=32448/208=156
Рассмотрим треугольник ABO, он
прямоугольный, тогда применим
теорему Пифагора:
AB2=BO2+AO2
AB2=1562+1042
AB2=24336+10816=35152
AB=√
BC=2AB=2*52√
Рассмотрим треугольник AOE.
OE=BE-BO=208-156=52
Так как этот треугольник тоже
прямоугольный, то можно применить
теорему Пифагора:
AE2=AO2+OE2
AE2=1042+522=10816+2704=13520
AE=√
Так как BE -
биссектриса, то используя ее
первое свойство запишем:
BC/AB=CE/AE
104√
2=CE/(52√
CE=104√
AC=AE+CE=52√
Ответ: AB=52√
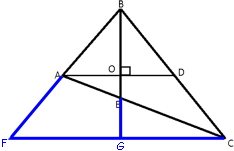 Проведём через точку C прямую, параллельную AD. Продлим BA и BE до пересечения с этой прямой в точках F и G соответственно.
Проведём через точку C прямую, параллельную AD. Продлим BA и BE до пересечения с этой прямой в точках F и G соответственно.Поделитесь решением
Присоединяйтесь к нам...
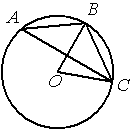 Точка О – центр окружности, /BOC=70° (см. рисунок). Найдите величину угла BAC (в градусах).
Точка О – центр окружности, /BOC=70° (см. рисунок). Найдите величину угла BAC (в градусах).
Косинус острого угла A треугольника ABC равен 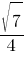 . Найдите sinA.
. Найдите sinA.
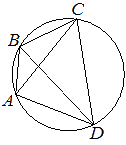 Четырёхугольник ABCD вписан в окружность. Угол ABC равен 138°, угол CAD равен 83°. Найдите угол ABD. Ответ дайте в градусах.
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 138°, угол CAD равен 83°. Найдите угол ABD. Ответ дайте в градусах.
 Тангенс острого угла прямоугольной трапеции равен 2/9. Найдите её большее основание, если меньшее основание равно высоте и равно 54.
Тангенс острого угла прямоугольной трапеции равен 2/9. Найдите её большее основание, если меньшее основание равно высоте и равно 54.
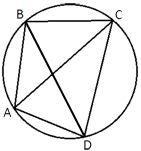 Четырехугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°. Найдите угол ABD. Ответ дайте в градусах.
Четырехугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°. Найдите угол ABD. Ответ дайте в градусах.
Комментарии:
(2017-03-30 22:54:26) Администратор: Артем, конечно, это опечатка, спасибо, что заметили. Исправлено.
(2017-03-28 23:06:43) Артём: Интересный треугольник рассматриваем в решении Всеволода, BOE)
(2017-03-15 23:51:16) Администратор: Евгений, я пишу по номерам для краткости. Эти номера можно найти, если нажать на ссылки в решении. На экзамене пишите так как от Вас требуют, а на сайте я публикую решения, чтобы учащиеся могли понять принцип, как решать подобные задачи. К примеру, иногда, тонкие моменты приходится особенно описывать, что на экзамене делать нет надобности.
(2017-03-15 16:18:58) Евгений: Исправьте пожалуйста свои задачи,не пишите по номеру признака или свойства т.к. на экзаменах надо писать подробно,а так путаница какая-то (в разных учебниках свойства и признаки под разными номерами)
(2017-02-07 19:39:58) Администратор: Данил, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, пишите, обязательно добавим.
(2017-02-07 19:13:39) Данил: AC и СВ-перпендикулярны прямой BD, точки A и C лежат по разные сторны прямой BD. докажите, что BC-паралельна AD, если AB=CD
(2015-10-28 20:56:44) Наталья: Спасибо, за Вашу работу, очень полезный сайт!!!!!
(2015-04-15 18:04:50) Администратор: Всеволод, я адаптировал и добавил Ваше решение.
(2015-03-16 01:30:56) Всеволод: Предлагаю чуть другое решение после того, как установили, что AB=BD. Проведём через точку C прямую, параллельную AD. Продлим BA и BE до пересечения с этой прямой в точках F и G соответственно. Получится равнобедренный треугольник BCF со средней линией AD и медианами BG и CA, которые в точке пересечения E делятся в отношении 2:1 считая от вершин. Раз BE=208, то EG=BE/2=104, вся BG=312, BO=OG=BG/2=156, OE=OG-EG=52. Далее так же: теорема Пифагора для треугольников ABO и AEO с известными катетами. Про CE=2EA уже упоминали (E -точка пересечения медиан), но это же следует и из свойств биссектрисы BE. (Спасибо за такой полезный сайт).